The Tiling Of Spectroscopy Plates
Tiling is the process by which the spectroscopic plates are designed and placed relative to each other. This procedure involves optimizing both the placement of fibers on individual plates, as well as the placement of plates (or tiles) relative to each other.
Because of large-scale structure in the galaxy distribution (which form the bulk of the SDSS targets), a naive covering of the sky with equally-spaced tiles does not yield uniform sampling. Thus, we present a heuristic algorithm for perturbing the centers of the tiles from the equally-spaced distribution to provide more uniform completeness. For the SDSS sample, we can attain a sampling rate of >92% for all targets, and >99% for the set of targets which do not collide with each other, with an efficiency >90% (defined as the fraction of available fibers assigned to targets).
Much of the content of this page can be found in the SDSS tiling paper; Blanton et al. 2003, AJ 125, 2276.
Jump to:
- Spectro Survey Overview
- What is tiling?
- Fiber Placement
- Dealing with Fiber Collisions
- Tile Placement
- Technical Details
- Tiling Window
The Spectroscopic Survey
The spectroscopic survey is performed using two multi-object fiber spectrographs on the same telescope. Each spectroscopic fiber plug plate, referred to as a “tile,” has a circular field-of-view with a radius of 1.49 degrees, and can accommodate 640 fibers, 48 of which are reserved for observations of blank sky and spectrophotometric standards. Because of the finite size of the fiber plugs, the minimum separation of fiber centers is 55”. If, for example, two objects are within 55” of each other, both of them can be observed only if they lie in the overlap between two adjacent tiles. The goal of the SDSS is to observe 99% of the maximal set of targets which has no such collisions (about 90% of all targets).
What is Tiling?
Around 2,000 tiles will be necessary to provide fibers for all the targets in the survey. Since each tile which must be observed contributes to the cost of the survey (due both to the cost of production of the plate and to the cost of observing time), we desire to minimize the number of tiles necessary to observe all the desired targets. In order to maximize efficiency (defined as the fraction of available fibers assigned to tiled targets) when placing these tiles and assigning targets to each tile, we need to address two problems. First, we must be able to determine, given a set of tile centers, how to optimally assign targets to each tile — that is, how to maximize the number of targets which have fibers assigned to them. Second, we must determine the most efficient placement of the tile centers, which is non-trivial because the distribution of targets on the sky is non-uniform, due to the well-known clustering of galaxies on the sky. We find the exact solution to the first problem and use a heuristic method developed by Lupton et al. (1998) to find an approximate solution to the second problem (which is NP-complete). The code which implements this solution is designed to run on a patch of sky consisting of a set of rectangles in a spherical coordinate system, known in SDSS parlance as a tiling region.
NOTE: the term “chunk” or “tiling chunk” is sometimes used to denote a tiling region.
Fiber Placement
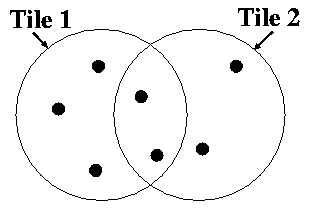
First, we discuss the allocation of fibers given a set of tile centers, ignoring fiber collisions for the moment. Figure 1 shows at the left a very simple example of a distribution of targets and the positions of two tiles we want to use to observe these targets. Given that for each tile there is a finite number of available fibers, how do we decide which targets get allocated to which tile? This problem is equivalent to a network flow problem, which computer scientists have been kind enough to solve for us already.
 |
 |
| Figure 1: Simplified Tiling and Network Flow View | |
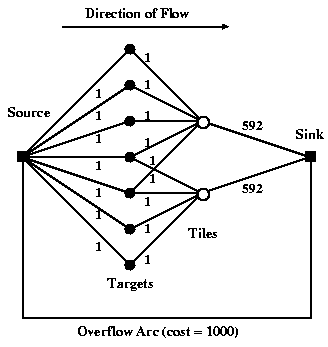
The basic idea is shown in the right half of Figure 1, which shows the appropriate network for the situation in the left half. Using this figure as reference, we here define some terms which are standard in combinatorial literature and which will be useful here:
- node: The nodes are the solid dots in the figure; they provide either sources/sinks of objects for the flow or simply serve as junctions for the flow. For example, in this context each target and each tile corresponds to a node.
- arc: The arcs are the lines connecting the nodes. They show the paths along which objects can flow from node to node. In Figure 1, it is understood that the flow along the arc proceeds to the right. For example, the arcs traveling from target nodes to tile nodes express which tiles each target may be assigned to.
- capacity: The minimum and maximum capacity of each arc is the minimum and maximum number of objects that can flow along it. For example, because each tile can accommodate only 592 target fibers, the capacities of the arcs traveling from the tile nodes to the sink node is 592.
- cost: The cost per object along each arc is exacted for allowing objects to flow down a particular arc; the total cost is the summed cost of all the arcs. In this paper, the network is designed such that the minimum total cost solution is the desired solution.
Imagine a flow of 7 objects entering the network at the source node at the left. We want the entire flow to leave the network at the sink node at the right for the lowest possible cost. The objects travel along the arcs, from node to node. Each arc has a maximum capacity of objects which it can transport, as labeled. (One can also specify a minimum number, which will be useful later). Each arc also has an associated cost, which is exacted per object which is allowed to flow across that arc. Arcs link the source node to a set of nodes corresponding to the set of targets. Each target node is linked by an arc to the node of each tile it is covered by. Each tile node is linked to the sink node by an arc whose capacity is equal to the number of fibers available on that tile. None of these arcs has any associated cost. Finally, an “overflow” arc links the source node directly to the sink node, for targets which cannot be assigned to tiles. The overflow arc has effectively infinite capacity; however, a cost is assigned to objects flowing on the overflow arc, guaranteeing that the algorithm fails to assign targets to tiles only when it absolutely has to. This network thus expresses all the possible fiber allocations as well as the constraints on the numbers of fibers in each tile. Finding the minimum cost solution then maximizes the number of targets which are actually assigned to tiles.
Fiber Collisions
As described above, there is a limit of 55” to how close two fibers can be on the same tile. If there were no overlaps between tiles, these collisions would make it impossible to observe ~10% of the SDSS targets. Because the tiles are circular, some fraction of the sky will be covered with overlaps of tiles, allowing some of these targets to be recovered. In the presence of these collisions, the best assignment of targets to the tiles must account for the presence of collisions, and strive to resolve as many as possible of these collisions which are in overlaps of tiles. We approach this problem in two steps, for reasons described below. First, we apply the network flow algorithm of the above section to the set of decollided targets — the largest possible subset of the targets which do not collide with each other. Second, we use the remaining fibers and a second network flow solution to optimally resolve collisions in overlap regions.
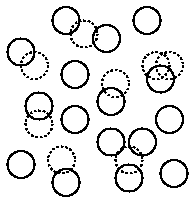
The “decollided” set of targets is the maximal subset of targets which are all greater than 55” from each other. To clarify what we mean by this maximal set, consider Figure 2. Each circle represents a target; the circle diameter is 55”, meaning that overlapping circles are targets which collide. The set of solid circles is the “decollided”set. Thus, in the triple collision at the top, it is best to keep the outside two rather than the middle one.
This determination is complicated slightly by the fact that some targets are assigned higher priority than others. For example, as explained in the targeting pages, QSOs are given higher priority than galaxies by the SDSS target selection algorithms. What we mean here by “priority” is that a higher priority target is guaranteed never to be eliminated from the sample due to a collision with a lower priority object. Thus, our true criterion for determining whether one set of assignments of fibers to targets in a group is more favorable than another is that a greater number of the highest priority objects are assigned fibers.
Once we have identified our set of decollided objects, we use the network flow solution to find the best possible assignment of fibers to that set of objects.
After allocating fibers to the set of decollided targets, there will usually be unallocated fibers, which we want to use to resolve fiber collisions in the overlaps. We can again express the problem of how best to perform the collision resolution as a network, although the problem is a bit more complicated in this case. In the case of binaries and triples, we design a network flow problem such that the network flow solution chooses the tile assignments optimally. In the case of higher multiplicity groups, our simple method for binaries and triples does not work and we instead resolve the fiber collisions in a random fashion; however, fewer than 1% of targets are in such groups, and the difference between the optimal choice of assignments and the random choices made for these groups is only a small fraction of that.
We refer the reader to the tiling algorithm paper for more details, including how the fiber collision network flow is designed and caveats about what aspects of the method may need to be changed under different circumstances.
Tile Placement
Once one understands how to assign fibers given a set of tile centers, one can address the problem of how best to place those tile centers. Our method first distributes tiles uniformly across the sky and then uses a cost-minimization scheme to perturb the tiles to a more efficient solution.
In most cases, we set initial conditions by simply laying down a rectangle of tiles. To set the centers of the tiles along the long direction of the rectangle, we count the number of targets along the stripe covered by that tile. The first tile is put at the mean of the positions of target 0 and target N_t, where N_t is the number of fibers per tile (592 for the SDSS). The second tile is put at the mean between target N_t and 2N_t, and so on. The counting of targets along adjacent stripes is offset by about half a tile diameter in order to provide more complete covering.
The method is of perturbing this uniform distribution is iterative. First, one allocates targets to the tiles, but instead of limiting a target to the tiles within a tile radius, one allows a target to be assigned to further tiles, but with a certain cost which increases with distance (remember that the network flow accommodates the assignment of costs to arcs). One uses exactly the same fiber allocation procedure as above. What this does is to give each tile some information about the distribution of targets outside of it. Then, once one has assigned a set of targets to each tile, one changes each tile position to that which minimizes the cost of its set of targets. Then, with the new positions, one reruns the fiber allocation, perturbs the tiles again, and so on. This method is guaranteed to converge to a minimum (though not necessarily a global minimum), because the total cost must decrease at each step.
In practice, we also need to determine the appropriate number of tiles to use. Thus, using a standard binary search, we repeatedly run the cost-minimization to find the minimum number of tiles necessary to satisfy the SDSS requirements, namely that we assign fibers to 99% of the decollided targets.
In order to test how well this algorithm works, we have applied it both to simulated and real data. These results are discussed in the tiling algorithm paper.
Technical Details
There are a few technical details which may be useful to mention in the context of SDSS data. Most importantly, we will describe which targets within the SDSS are “tiled” in the manner described here, and how such targets are prioritized. Second, we will discuss the method used by SDSS to deal with the fact that the imaging and spectroscopy are performed within the same five-year time period. Third, we will describe the tiling outputs which the SDSS tracks as the survey progresses. Throughout, we refer to the code which implements the algorithm described above as tiling.
Only some of the spectroscopic target types identified by the target selection algorithms in the SDSS are “tiled.” These types (and their designations in the primary and secondary target bitmasks) are described in the targetting pages). They consist of most types of QSOs, main sample galaxies, LRGs, hot standard stars, and brown dwarfs. These are the types of targets for which tiling is run and for which we are attempting to create a well-defined sample. Once the code has guaranteed fibers to all possible “tiled targets,” remaining fibers are assigned to other target types by a separate code.
All of these target types are treated equivalently, except that they assigned different “priorities,” designated by an integer. As described above, the tiling code uses them to help decide fiber collisions. The sense is that a higher priority object will never lose a fiber in favor of a lower priority object. The priorities are assigned in a somewhat complicated way for reasons immaterial to tiling, but the essence is the following: the highest priority objects are brown dwarfs and hot standards, next come QSOs, and the lowest priority objects are galaxies and LRGs. QSOs have higher priority than galaxies because galaxies are higher density and have stronger angular clustering. Thus, allowing galaxies to bump QSOs would allow variations in galaxy density to imprint themselves into variations in the density of QSOs assigned to fibers, which we would like to avoid. For similar reasons, brown dwarfs and hot standard stars (which have extremely low densities on the sky) are given highest priority.
Each tile, as stated above, is 1.49 degrees in radius, and has the capacity to handle 592 tiled targets. No two such targets may be closer than 55” on the same tile.
The operation of the SDSS makes it impossible to tile the entire 10,000 square degrees simultaneously, because we want to be able to take spectroscopy during non-pristine nights, based on the imaging which has been performed up to that point. In practice, periodically a “tiling region” of data is processed, calibrated, has targets selected, and is passed to the tiling code. During the first year of the SDSS, about one tiling region per month has been created; as more and more imaging is taken and more tiles are created, we hope to decrease the frequency with which we need to make tiling regions, and to increase their size.
A tiling region is defined as a set of rectangles on the sky (defined in survey coordinates). All of these rectangles cover only sky which has been imaged and processed. However, in the case of tiling, targets may be missed near the edges of a tiling region because that area was not covered by tiles. Thus, tiling is actually run on a somewhat larger area than a single tiling region, so the areas near the edges of adjacent tiling regions are also included. This larger area is known as a tiling region. Thus, in general, tiling regions overlap.
The first tiling region which is “supported” by the SDSS is denoted Tiling Region 4. The first tiling region for which the version of tiling described here was run is Tiling Region 7. Tiling regions earlier than Tiling Region 7 used a different (less efficient) method of handling fiber collisions. The earlier version also had a bug which artificially created gaps in the distribution of the fibers. The locations of the known gaps are given in the EDR paper for Tiling Region 4 as the overlaps between plates 270 and 271, plates 312 and 313, and plates 315 and 363 (also known as tiles 118 and 117, tiles 76 and 75, and tiles 73 and 74).
Tiling Window
In order to interpret the spectroscopic sample, one needs to use the information about how targets were selected, how the tiles were placed, and how fibers were assigned to targets. We refer to the geometry defined by this information as the “tiling window” and describe how to use it in detail below.
When one is given a set of spectra from any survey, and one wants to ask statistical questions about them, the first thing one should ask is “How were these objects selected?” The SDSS is designed such that one can answer this question easily for the tilable targets (for the most part QSOs, Main Sample galaxies, and Luminous Red Galaxies). The answer has several steps:
- Photometric detection (requires understanding the photometric imaging mask)
- Target selection (requires understanding the target selection algorithms)
- Tiling (the algorithm is described above)
- Spectroscopic completeness (whether or not a spectrum successfully yields a classification)
This section addresses the second and third aspects: how tilable targets are selected and assigned to each tile.
The way to understand the tiling window is as follows. In each direction of the sky we can ask two questions:
- what version of the target algorithm was used in this direction (for example, to determine the flux limit in the targeted data)?
- what set of tiles had the opportunity to put a fiber on a target in this direction?
Once one can answer these two questions, one can define a complete spectroscopic sample from the SDSS. The second question, in detail, is not the same as asking whether the direction in question is within 1.49 deg of the tile center in question. This is because tiles near edges of tiling regions (that is, virtually all tiles) extend beyond the tiling region area. In some cases, the survey then later observed and targeted the adjacent area. This fact, and the generally complex geometry which results from the survey configuration, make the expression of the window function nontrivial. However, these geometric problems have been solved and the solutions are included in the data release.
To demonstrate the SDSS procedure, consider the following figures, which represent how targets were selected and how tiles were defined along a section of the SDSS near the Northern Celestial Equator. The region shown was successively targeted in Tile Region 4, Tile Region 5 and Tile Region 14. The images show:
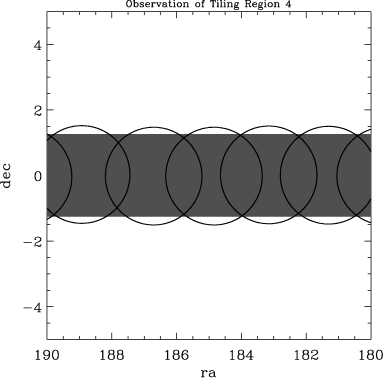
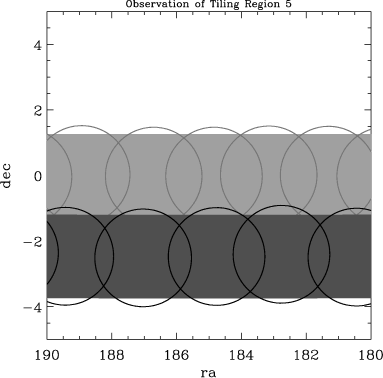
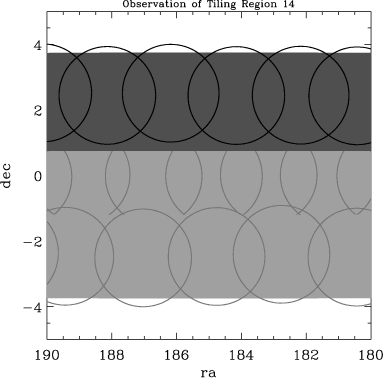
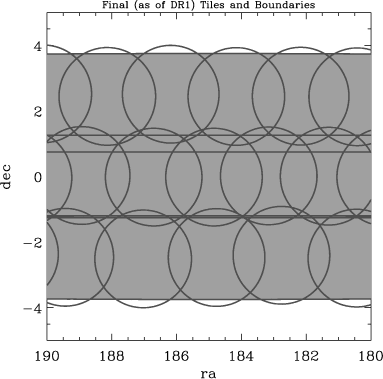
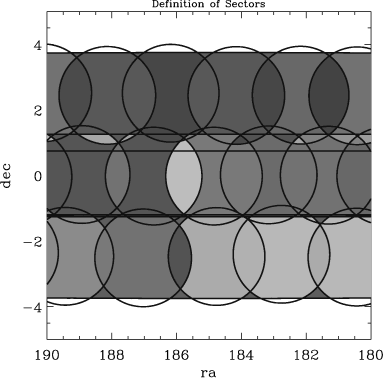
Since the SDSS is so complete, the details of exactly which set of tiles covered any given region would not be important, except that in certain cases there are resulting gaps, which are important to track.
The Catalog Archive Server provides all tiling information needed to interpret the details of the above geometry.
The tiling window describes only how tiling treats the geometry for the relevant set of data released here. It does not account for decisions about the photometric window released here or for fields identified as bad since the era of targeting. So in addition to the tiling window, one needs to also account for:
- the fact that targets 100 arcsec from the tile center are excluded
- the photometric window (including bad fields) of the data release
- which tiles had corresponding plates released
This information can be acquired elsewhere in this data release documentation, as referenced at the beginning of this page.



