APOGEE Stellar Parameter and Chemical Abundance Pipeline (ASPCAP)
One main objective of the APOGEE survey is to extract the chemical abundances of several elements for the entire stellar sample. This is achieved by comparing APOGEE observations to a large library of synthetic spectra and determining the best matching synthetic spectrum, allowing for interpolation within the library. To determine the elemental abundances, the stellar atmospheric parameters — effective temperature, surface gravity, overall metallicity, microturbulent and macroturbulent velocities, and rotation — must be known. The APOGEE Stellar Parameters and Chemical Abundances Pipeline (ASPCAP) employs a two-step process to extract abundances: first, determination of the atmospheric parameters by fitting the entire APOGEE spectrum, and second, use of these parameters to fit limited regions of the spectrum dominated by spectral features associated with a particular element in order to derive the individual element abundance ([X/H] or [X/M], see below).
APOGEE uncertainties
APOGEE reports uncertainties as standard deviations.
This is in contrast to the optical spectral pipelines (such as the Optical Spectroscopy Pipeline or the SEGUE Stellar Parameter Pipeline), which typically report uncertainties as inverse variances.
The wavelength region covered by the APOGEE spectra includes a vast number of atomic transitions of many elements, but molecular features, in particular, from CN, CO, and OH can be very prominent, especially in cooler stars that comprise the bulk of the survey sample. A global fit needs to include the possibility of variations in elemental abundance ratios that have a significant effect in the equation of state (e.g. through CO formation or contributing free electrons) or the opacity. For this reason, the stellar parameters portion of the ASPCAP pipeline has the potential to allow for variations in nine parameters: effective temperature, surface gravity, microturbulence, macroturbulence, rotation, overall metal abundance [M/H] , relative α-element abundance [α /M] (defined as O, Mg, Si, S, Ca, and Ti changing with solar proportions in lockstep), carbon [C/M], and nitrogen [N/M] abundances. For giant stars, this is simplified by deriving relations for microturbulence and macroturbulence as a function of the basic stellar parameters (surface gravity and metallicity); for dwarf stars, this is simplified by the assumption that solar abundance ratios for carbon and nitrogen are sufficient for the global stellar parameter fits (carbon and nitrogren abundances are still derived separately during the abundance determinations).
For a discussion of the quality of the derived parameters, and important things to know about using them, all users of ASPCAP results should read Using APOGEE stellar parameters. For a discussion of the quality of the individual elemental abundances, and important things to know about using them, all users of ASPCAP results should read Using APOGEE chemical abundances.
For additional information on ASPCAP, consult Garcia-Perez et al. (2015).
The APOGEE abundance scale
The abundance of each individual element X heavier than helium, is defined as
where nX and nH are respectively the number of nuclei of element X and hydrogen, per unit volume in the stellar photosphere. We define [M/H] as an overall scaling of the metal abundance pattern in the Sun, and therefore [X/M] different from zero involves deviation of the abundance of element X from the solar abundance pattern:
Once the stellar parameters have been determined, abundances for individual elements are derived individually, by fitting the spectrum in limited spectral windows that contain features of the desired element (see the section on abundances below).
Some caveats apply. The abundances are NOT truly differential to the Sun. Solar abundances are adopted from Asplund et al. (2005), and used for computing model atmospheres (see Mészáros et al. 2012) and synthetic spectral grids. The line list used for spectral synthesis includes, in addition to laboratory and theoretical transition probabilities and damping constants, modifications to match the solar spectrum and that of the red giant Arcturus. Please consult Shetrone et al. (2015) for further details.
APOGEE DR13 also includes a spectrum of the Sun observed through reflected light on the asteroid Vesta, and also a spectrum of Arcturus observed using the NMSU 1m telescope in conjunction with the APOGEE instrument. These allow some independent checks of the abundance scale.
In DR13, we provide the best fitting values of the global stellar parameters as well as individual elemental abundances for C, N, O, Na, Mg, Al, Si, P, S, K, Ca, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Ge, Rb. The raw measurements from the fits to the spectral grid are internally calibrated (small temperature-dependent corrections), predominantly using observations of stellar clusters. In DR13, the abundances are calibrated by forcing the mean abundance of stars near the solar circle that have overall metal abundance near the solar abundance to be the solar abundance. For more details, see the section on calibration below.
APOGEE Stellar Parameters and Chemical Abundances Pipeline (ASPCAP)
ASPCAP Steps
- Large grids of synthetic spectra are computed for the APOGEE wavelength region, using a custom linelist derived for this portion of the spectrum. The grids cover the full expected range of the nine parameters mentioned above: Teff, log g, vmicro, vmacro, vsini, [M/H], [α/M], [C/M], and [N/M]. The synthetic spectra are “pseudo-continuum normalized” by iterative fitting by least squares and sigma-clipping a polynomial to the fluxes. The sigma clipping has asymmetric limits for rejection, rejecting more vigorously lower points, with the goal of pushing the polynomial to the upper envelope of the spectrum.
- Combined APOGEE spectra are pseudo-continuum normalized to remove variations of spectral shape arising from interstellar reddenning, errors in relative fluxing, and atmospheric absorption. This normalization is done the same way as for the synthetic spectra, so that they can be directly compared (the true continuum level is hard to determine from the observed spectra).
- An independent code ( FERRE — see Allende Prieto et al. 2006) searches for the best matching synthetic spectrum for each star via χ2 minimization technique, allowing for interpolation in the synthetic spectra grid.
- From the results of the different synthetic grids, the best-fit synthetic spectrum is identified for each object, and the best-fitting results for all of the stars are compiled.
- Using the best-fit parameters, small windows around features of specific individual elements are fit to derive the elemental abundances.
- Internal calibration relations are applied that make small temperature-dependent corrections to the abundances; these were derived by looking at abundances as a function of temperature within (mostly metal-rich, open) clusters, under the assumptions that these clusters have homogeneous abundances. Using results from the derived parameters for objects of known parameters, some external calibration relations have been derived, and these relations are applied to some of the derived parameters. In addition, this stage sets a series of data quality flags for the stellar parameter and abundances results.
This procedure works only as well as the synthetic spectra match the observed data, and to the degree that the observed data contain parameter and abundance information. At cooler temperatures (T<4000K) the model spectra do not match as well, so parameters and abundances there are currently less certain. At warmer temperatures (T>5500 K), spectral features of some elements become very weak, so their measurement is significantly less certain.
Stellar Spectral Libraries
Grids of normalized stellar synthetic spectra are computed with the spectral synthesis code
Turbospectrum ( Alvarez and Plez 1998; Plez 2012), using ATLAS9 (or MARCS) model atmospheres described by Mészáros et al. 2012 (see also Zamora et al 2015), and a line list for the APOGEE wavelength region compiled from the literature and tuned to match the spectrum of the Sun (see Shetrone et al. 2015). The model atmospheres and the synthetic spectra adopt solar abundances by Asplund et al. 2005, but with varying metallicities, carbon, and α-element abundances. Variations in nitrogen abundances are also considered, but only at the synthesis stage (not in the model atmospheres). A comparison between spectra computed with ATLAS9 model atmospheres and the ASSET ( Zamora et al. 2015).
Ideally we would store the entire grid of stellar spectra in memory to allow for efficient computation comparison between observed and interpolated model spectra. However, the multi-dimensional synthetic spectrum library is too large to store simultaneously in the memory of a typical computer. For this reason, the flux arrays are compressed using Principal Component Analysis, and the full parameter space is split into different grids that cover different temperature regimes. For DR13 we use five grids: a GK giant grid which covers 3500-6000 K with giant-like CNO isotopic ratios, a GK dwarf grid which covers 3500-6000 K with solar isotope ratios, the F grid which covers 5500-8000 K with solar isotope ratios, a M giant grid which covers 2500-4000 K with giant isotope ratios, and a M dwarf grid that covers 2500-4000K with solar isotope ratios. Note that the GK and F grids are based on ATLAS9 model atmospheres, while the cooler M grids are based on MARCS atmospheres.
To determine the final grid, a coarse run is performed with the F, GK giant, and M giant grids is done, fixing the abundance ratios C/Fe and N/Fe to solar values, and the results are used to decide what grid(s) for a full run. If more than one grid is used, then the grid that produces the best fit is adopted; however, in the range 3500<Teff<4000 K, we force the use of the GK grid over the M grid, so that results are uniform over this temperature range.
In general, many parameters may be required to adequately describe the spectra, but for warm stars (Teff>6000 K) there is not sufficient information in the APOGEE spectra to independently determine all of those parameters. In addition there are instances in which full fits including all of the relevant parameters is computationally expensive and therefore some compromises are made.
For the giant grids, [C/M] and [N/M] are retained as separate dimensions, but fixed relations for microturbulent and macroturbulent velocity are adopted and rotation is not included. The adopted relation for microturbulence for giants is:
The adopted relation for macroturbulent velocity for giants is:
These relations were derived from a calibration subsample of APOGEE spectra, sequentially: first a relation for microturbulence was derived, then one for macroturbulence. The full sample was then analyzed using the resulting 6D grid.
For the dwarf grids, the relative carbon and nitrogen abundances are fixed to solar values, i.e., [C/M]=[N/M]=0, for the parameter determination, and microturbulent velocity and rotation are retained as independent dimensions. This also results in a 6D grid.
The synthetic spectra are smoothed using a line spread function (LSF) measured from APOGEE sky spectra. However, the LSF varies with wavelength and location in the frame. In DR13, we have made a first effort to account for this by creating four different library versions for different groups of mean fiber number for each star (stars are observed with different fibers in different visits); (note that DR12 used a single average LSF). After smoothing, the library spectra are interpolated onto the same wavelength scale as the combined APOGEE spectra, and pseudocontinuum normalized.
The following table summarizes the synthetic grids:
| Class | Dimensions | Teff | log g | log vmicro | log vmacro | log vrot | [M/H] | [C/M] | [N/M] | [α/M] |
|---|---|---|---|---|---|---|---|---|---|---|
| GK giant | 6 | 3500 to 6000 | 0 to 5 | f(log g) | f(log g,[M/H]) | 0. | -2.5 to 0.5 | -1 to 1 | -1 to 1 | -1 to 1 |
| step: 250 | step: 0.5 | … | … | … | step: 0.5 | step: 0.25 | step: 0.5 | step: 0.25 | ||
| GK dwarf | 6 | 3500 to 6000 | 0 to 5 | -0.301 to 0.903 | 0. | 0.176 to 1.982 | -2.5 to 0.5 | -1 to 1 | -1 to 1 | -1 to 1 |
| step: 250 | step: 0.5 | step: 0.301 | … | step: 0.301 | step: 0.25 | step: 0.25 | step: 0.5 | step: 0.25 | ||
| M giant | 6 | 2500 to 4000 | -0.5 to 5 | f(log g) | f(log g, [M/H]) | … | -2.5 to 0.5 | -1 to 1 | -1 to 1 | -1 to 1 |
| step: 100 | step: 0.5 | … | … | … | step: 0.5 | step: 0.5 | step: 0.5 | step: 0.5 | ||
| M dwarf | 6 | 2500 to 4000 | -0.5 to 5 | -0.301 to 0.903 | 0. | 0.176 to 1.982 | -2.5 to 0.5 | -1 to 1 | -1 to 1 | -1 to 1 |
| step: 100 | step: 0.5 | step: 0.301 | … | step: 0.301 | step: 0.5 | step: 0.5 | step: 0.5 | step: 0.5 | ||
| F | 6 | 5500 to 8000 | 1 to 5 | -0.301 to 0.903 | 0. | 0.176 to 1.982 | -2.5 to 0.5 | -1 to 1 | -1 to 1 | -1 to 1 |
| step:250 | step: 0.5 | step: 0.301 | … | step: 0.301 | step: 0.25 | step: 0.25 | step: 0.5 | step: 0.25 |
ASPCAP Pre-processing
The comparison of observations with the library requires the pre-processing of the combined APOGEE spectra, which is carried out by an IDL wrapper, and consists of masking out bad pixels and normalizing the spectra.
- Since FERRE minimizes χ2, realistic estimates of flux uncertainties are critical, and any bad data must be masked. Pixels flagged as bad (saturated, cosmic ray, etc) in the data-reduction process and pixels around the sky emission lines are ignored for continuum normalization, and in the χ2 minimization. To account for small systematic errors in spectral calibration, we set a minimum error of 0.5 percent for all pixels.
- To normalize the spectra, the spectral regions covered by each of the three chips used in the APOGEE spectrograph are considered separately. In each region, a sigma-clipping algorithm is used to fit a polynomial to the upper envelope of the spectrum. In order to allow a meaningful comparison to the library of synthetic spectra, an identical normalization is performed on the library, using the same spectral regions with the same sigma-clipping and polynomial form. We emphasize that this normalization is not a normalization to the true continuum, because, especially for metal-rich stars, the upper envelope of the data may still not be at the true continuum level. Thus, we do not calculate abundances from equivalent widths from these “pseudo-continuum” normalized spectra, but rather comparing to models that have had the same normalization procedure applied.
Determination of stellar parameters (FERRE)
Stellar parameters and the relative abundances of C, N and α-elements are determined by the FORTRAN90 code FERRE, which compares the observations with the grid of pre-computed synthetic spectra. The code uses a χ2 criterion as the merit function, and searches for the best matching synthetic spectrum using the Nelder-Mead algorithm (Nelder and Mead 1965). The search is run 12 times starting from different locations: the center of the grid for [C/M], [N/M] and [α/M], and at two different places symmetrically located from the grid center for [M/H] and log g, and at three for Teff. Interpolation within the grid of synthetic spectra is accomplished using cubic Bezier interpolation. The code returns the best matching spectrum, the parameters associated with that spectrum (stellar parameters and [C/M], [N/M] and [α/M] abundance ratios), the covariance matrix of these parameters, and the χ2 value for the best-matching spectrum.
Abundance determination
The abundance derivation takes place after the atmospheric parameters (Teff, log g, vmicro, [M/H], [α/M], [C/M], and [N/M]) have been simultaneously determined from the APOGEE spectra. A second call to the optimization program (FERRE) is performed for the abundance determination. For these fits, the same library of synthetic spectra is used, but with two main changes:
- Abundances of individual alpha elements (O, Mg, Si, S, Ca, and Ti) are derived by varying the [α/M] dimension of the grid, the abundance of carbon and nitrogen by varying the [C/M] and [N/M] dimensions (in the giant grids; in the dwarf grids C and N are derived using the [M/H] dimension), and the abundances of all other elements by varying the [M/H] dimension. All other atmospheric parameters are held at the values previous determined.
- The weights for the chi-square calculations are now changed so that we only consider spectral features that are primarily sensitive to the element we are interested in. The assumption here is that, within the defined windows (see below), the abundance of the desired element dominates over variations from other elements contained in the same grid dimension.
Therefore, we are not really changing the element of interest only, but the element of interest and others: all α elements as a block when fitting an α element, or all metals when changing a non-α element. This approach works well when the abundance we derive is not very different from the group it belongs to (either just the α elements, or all metals).
Transitions used (weight determination)
Deriving the relevant weights for each element is basically equivalent to deciding which transitions and which parts of the line profiles are to be used for each element.
This is accomplished by using first a algorithm that evaluates the derivatives of the model fluxes with respect to each elemental abundance for a star like Arcturus (Teff=4300 K, logg=1.7, [Fe/H]=-0.5). Frequencies (wavelengths) at which the amplitude of the derivative for the element of interest is large are given a high weight, with a negative contribution when the module of the derivatives are large for any other element in the same element family. Weights are adjusted with a multiplicative factor that takes into account how well the model spectrum for Arcturus reproduces an actual observation of this star. A second multiplicative factor takes into account how well APOGEE spectra are reproduced by the model fluxes, using the median residuals at each frequency based on fitting the entire APOGEE sample.
The number of transitions/features used for each element varies from element to element: there are 45 for C (C I, but mainly CO and CN), 77 for N (CN), 50 for O (OH), 2 for Na (Na I), 4 for Mg (Mg I), 2 for Al (Al I), 10 for Si (Si I), 3 for S (S I), 5 for P, 1 for K (K I), 3 for Ca (Ca I), 9 for TiI (1 for Ti II), 2 for V (V I), 7 for Cr, 4 for Mn (Mn I), 61 for Fe (Fe I), 7 for Ni (Ni I), 4 for Co, 2 for Co, 1 for Ge, and 1 for Rb. However, these numbers do not reflect the number of transitions in a window, the different strengths of the features, and the degree to which they are blended with other features. The attached pdf file shows the fittings for the observations of Arcturus in the Hinkle et al. (1995) atlas (smoothed with a Gaussian profile to R~22,500) and this one is the equivalent for the APOGEE observation of the same star from thee APO 1m telescope (with 4 Fe I transitions illustrated in the figure).
ASPCAP post-processing
Once FERRE has delivered results for the different temperature grids, the IDL wrapper chooses the result that produces the lowest χ2. These results (pseudo continuum, normalized observed spectra, flux errors, stellar parameters and [C/M], [N/M], [α/M] values, covariance matrix, χ2 values) along with other relevant information (e.g. 2MASS photometry, reddening, radial velocities, signal-to-noise ratios etc.) are compiled.
Calibration and Final Error Estimates of the Parameters
In addition to the raw FERRE output parameters, we also provide a calibrated set of parameters. Temperatures and surface gravities are calibrated relative to independent measurements of these quantities in a calibration subset. Abundances are internally calibrated to provide homogeneous results within clusters and are externally calibrated to force solar metallicity stars in the solar circle to have solar abundances on average.
Internal calibration
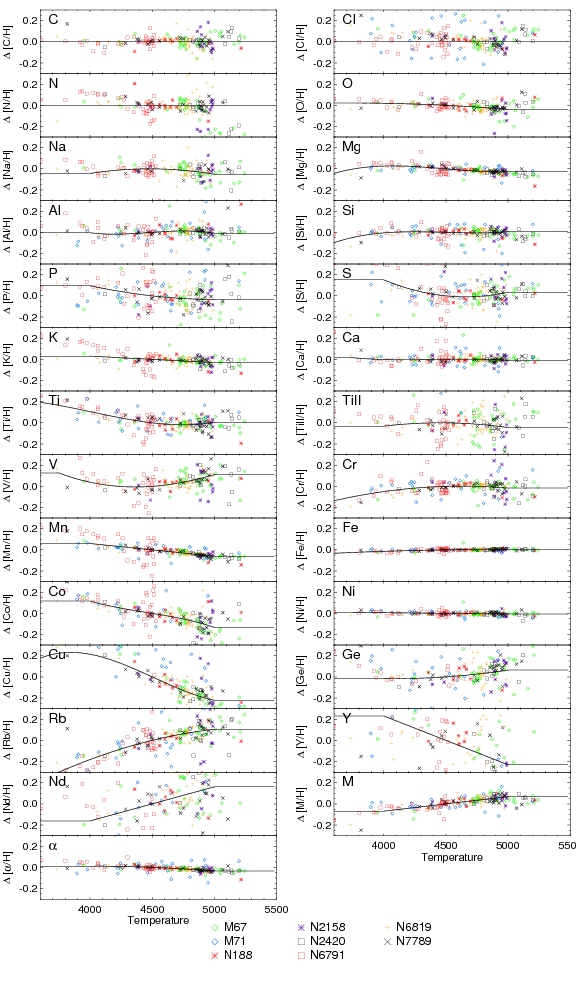
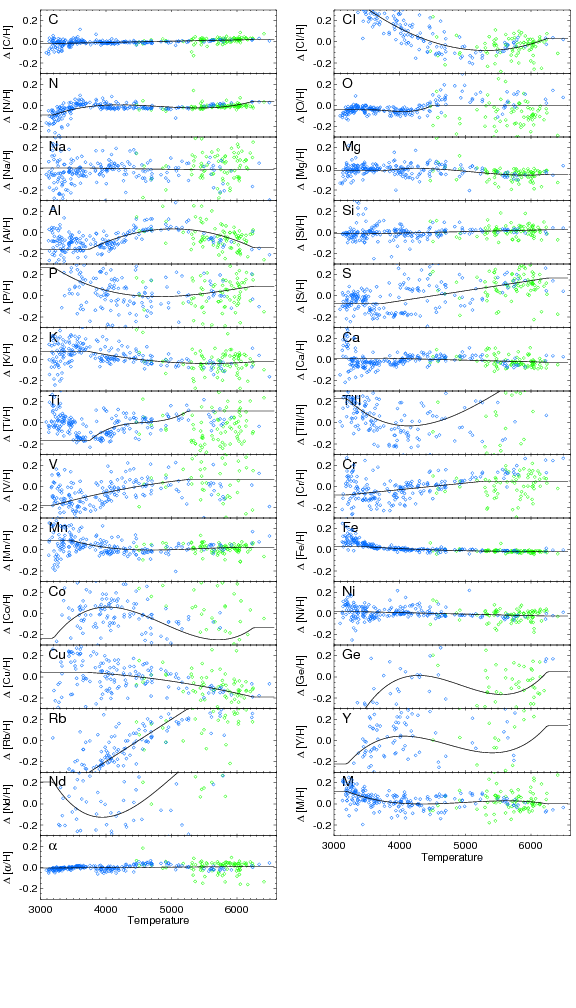
The abundance parameters ([M/H] and [α/M]), as well as all of the individual element abundances are internally calibrated based on observations of stellar clusters with [Fe/H]>-1. Under the assumption that such clusters have internally homogeneous abundances, we find small systematic variations of abundance with temperature, and use these to derive internal calibration relations of the form:
(although not all terms are used for all elements) to provide internally calibrated abundances. We obtain separate calibration relations for giants and for dwarfs. For giants, we do not do any calibration for carbon and nitrogen, since these are known to have varying abundances due to mixing along the giant branch.
For giants, the calibration sample is restricted in effective temperature range from around 3800K to 5250K; for sample stars outside this range, we apply the correction at the edge of the range (i.e., we don’t extrapolate the relation), and set a bit (CALRANGE_WARN) in the abundance flags.
Note that results for Nd and Y suggest that no useful information on these elements is being extracted, so we do not present any calibrated abundances for these.
External calibration
The adopted external calibrations are summarized here:
- Accuracy of the ASPCAP effective temperatures have been judged by comparing to temperatures obtained from photometric temperatures (e.g., González Hernández and Bonifacio (2009) IRFM scale) for a low-reddening sample of giants. In general, it appears that the ASPCAP temperatures are relatively close to those expected from the colors for the bulk of the sample, which is near solar metallicity. As a result, and because of potential uncertainties in the photometric metallicity scale, we made the choice not to apply any calibration to the derived effective temperatures; this differs from DR12, where we applied an offset of about 90 K, so the raw and calibrated effective temperatures are identical.
Subsequent to the freezing of DR13, however, we recognized that there does seem to be a significant trend in the difference between the spectroscopic temperature and photometric temperatures that is a function of metallicity. See the Using parameters for more details and a recommended adjustment.
- Corrections for the surface gravities were estimated from a set of stars observed in the Kepler field, for which asteroseismic analysis yields highly accurate surface gravities. There is an apparent offset in the derived calibration from red giant (RGB) and red clump (RC) stars that is currently not well-understood. Since we now have a large sample of stars with asteroseismic surface gravity measurements, we apply separate calibrations for RGB and RC stars. For RGB stars, we use
log g = log gASPCAP – ( 0.300 – 0.048 log g + 0.147 [M/H])
while for RC stars, we use
log g = log gASPCAP – ( -4.442 + 3.326 log g + 0.147 [M/H] – 0.581 (log g)2)We attempt to distinguish between RGB and RC stars on the basis of the raw ASPCAP stellar parameters. For every star, we compute the temperature difference between the derived temperature and a fiducial metallicity-dependent ridgeline derived by Bovy et al. (2014):
Tridge = 4468+(log g-2.5)/0.0018 – 382.5 [M/H]Stars cooler than the ridgeline temperature are classified as RGB stars, while stars more than 100 K hotter than the ridgeline temperature are classified as RC stars. For stars in the intermediate region, the observed C/N ratio is used to help to discriminate RGB from RC stars.
Stars with[C/N] < -0.113-0.0043 (T-Tridge)are classified as RGB stars, while stars with
[C/N] > -0.088-0.0018 (T-Tridge)For stars in an ambiguous region in C/N space, we interpolate between the RGB and RC corrections.
Subsequent to the freezing of DR13, however, we recognized that there appears to be a systematic offset
in the calibrated surface gravities for stars with [M/H]<-1.5. See the Using parameters for more details and a recommended adjustment. - The parameter-level [α/M] and the individual elemental abundances have been externally calibrated by separately determining the mean abundances ([X/M]) of stars with near-solar metallicity (-0.1<[M/H]<0.1) dwarfs and giants in a restricted range of Galactic longitude (70<l<110), in an effort to restrict stars to those near the Solar circle. Since previous studies have shown that stars in the solar neighborhood typically have solar abundance ratios at solar metallicity, we apply an offset to the individual [X/M] abundances to force this to be true for the APOGEE measurements.
- Empirical parameter and abundance uncertainties have been estimated based on scatter observed within clusters. See the abundance uncertainty section of the Using Abundances page for additional details.
Output data files
ASPCAP is generally run separate for each APOGEE field (i.e. location in the sky). The ASPCAP output for all stars in the field is stored in a single aspcapField file. Results for each individual star are stored in aspcapStar files. See the links for a full description of the data in these files, but briefly, the aspcapField files are binary FITS tables that contain three separate tables: the first contains the information about the star and the derived stellar parameters, the second contains the observed and best-matching synthetic spectra, and the third contains library and wavelength information; aspcapStar files are FITS image files with the spectrum, the uncertainty, and the best fitting synthetic spectrum for the star.
All of the derived parameters and abundances are stored in the master allStar file with contents described in the allStar datamodel.