Stellar Population Models
Spectro-Photometric Model Fitting
The stellar population models of Maraston (2005) and Maraston et al. (2009) are used to perform a best-fit to the observed ugriz magnitudes of BOSS galaxies with the spectroscopic redshift determined by the BOSS pipeline, using an adaptation of the publicly available Hyper-Z code of Bolzonella, Miralles & Pelló (2000). The fit is carried out on extinction corrected model magnitudes that are scaled to the i-band c-model magnitude, i.e.:
mag_x = modelmag_x - extinction_x + (cmodelmag_i - modelmag_i),
where x denotes the photometric band (ugriz).
Two sets of template spectra are used (see Maraston et al. 2012 for details):
- a passively evolving galaxy with a two-component metallicity of same age and no ongoing star formation or reddening, as in Maraston et al. (2009),
- an ensemble of canonical star formation modes, including exponentially-declining, constant with truncation, and constant, star formation, for various timescales and various metallicities, as in Maraston et al. (2006). In order to minimize the event of low-age, high-dust fake solutions, reddening is not included (Pforr, Maraston & Tonini 2012 [submitted to MNRAS]). Both template sets are available for Salpeter and Kroupa initial mass functions.
The output of the fit for each galaxy includes: age, star formation mode, metallicity, k-corrected absolute magnitudes in ugriz, plus the reduced χ2. Additionally, the best fit model spectrum as well as the probability distribution function (PDF) for the stellar mass are provided. Stellar masses and star formation rates are computed from the best-fit SED as in Maraston et al. (2006). Furthermore the stellar mass at the median PDF and 68% confidence levels are provided. Mass loss due to stellar evolution and the account of mass in stellar remnants is included.
The algorithm assumes a ΛCDM cosmology with H0 = 71.9, Ωm = 0.258, and ΩΛ = 0.742.
Emission Line Kinematics
An adaptation of the publicly available Gas AND Absorption Line Fitting (GANDALF, Sarzi et al. 2006) and penalised PiXel Fitting (pPXF, Cappellari & Emsellem 2004) codes are used to fit the stellar population synthesis models of Maraston & Strömbäck (2011) and Thomas, Maraston & Johansson (2011) to observed BOSS galaxy spectra. We chose these codes as GANDALF simultaneously fits stellar templates and Gaussian emission-line models.
The stellar population synthesis models used were all at fixed solar metallicity to limit computing time, utilised the MILES stellar library and had age ranges from 6.5 Myr to 11 Gyr. Since we were not using this fit to extract stellar population metallicities and ages, considering only solar metallicity did not impact on our results and age-metallicity degeneracy effects were unimportant. We adopted the MILES resolution calculated in Beifiori et al. (2011).
Outputs from this fitting process that we are providing include the emission-line fluxes (both observed and de-reddened) and equivalent widths, the gas kinematics, the stellar kinematics, an E(B-V) value and derived BPT classifications. Our reddening values can be obtained by plugging the E(B-V) value for each object into the dust attenuation equation of Calzetti et al. (2000).
Outputs from this fitting process that we are providing include the emission-line fluxes (both observed and de-reddened) and equivalent widths, the gas kinematics, the stellar kinematics, two E(B-V) values (explained below), absorption line indices and derived BPT classifications.
A reduced χ2 value is also provided for the fit, as well as Amplitude-over-Noise (AoN) values for each of the emission lines.
Principal Component Analysis (PCA) Method
Chen et al. (2012) model physical galaxy parameters based on a library of model spectra for which principal components (PCs) have been identified. The method is applied in the following steps.
Create library of model spectra
The library of model spectra is based on Bruzual & Charlot (2003) stellar population synthesis models. The model is parameterized by the following characteristics.
Star formation histories (SFHs)
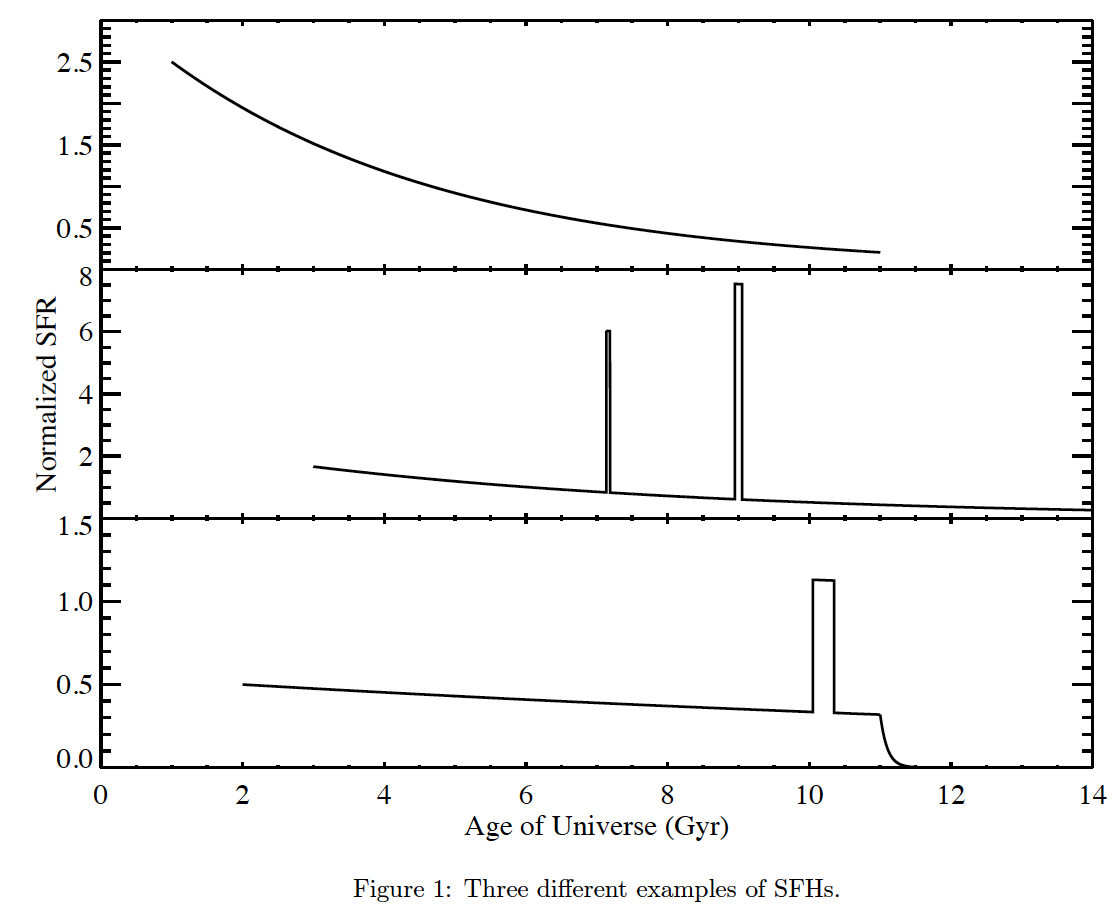
Each SFH consists of three parts: an underlying continuous model + a series of super-imposed stochastic bursts + a random probability for star formation to stop exponentially (i.e. truncation). Figure 1 shows three examples of SFHs. The top panel is a continuous model, middle panel shows a continuous model with two random bursts, a truncation can be found in the bottom panel.
Metallicity
95% of the model galaxies in the library are distributed uniformly in metallicity from 0.2 – 2.5 Z☉; 5% of the model galaxies are distributed uniformly between 0.02 and 0.2 Z☉.
Dust extinction
Dust extinction is modelled using the two-component model described in Charlot & Fall (2000). The V-band optical depth has a Gaussian distribution over the range 0 < τV < 6. with a peak at 1.2 and 68% of the total probability distribution distributed over the range 0~2. This prior distribution of τV values is motivated by the observed distribution of Balmer decrements in SDSS spectra (Brinchmann et al. 2004). The fraction of the optical depth that affects stellar populations older than 0.01 Gyr is parametrized as μ, which is again modeled as a Gaussian with a peak at μ = 0.3, and a 68 percentile range of 0.1~1.
Velocity dispersion
Each of the model spectra is convolved to a velocity that is uniformly distributed over the range of values from 75 to 400 km/s.
Principal components (PCs) are identified from the model library
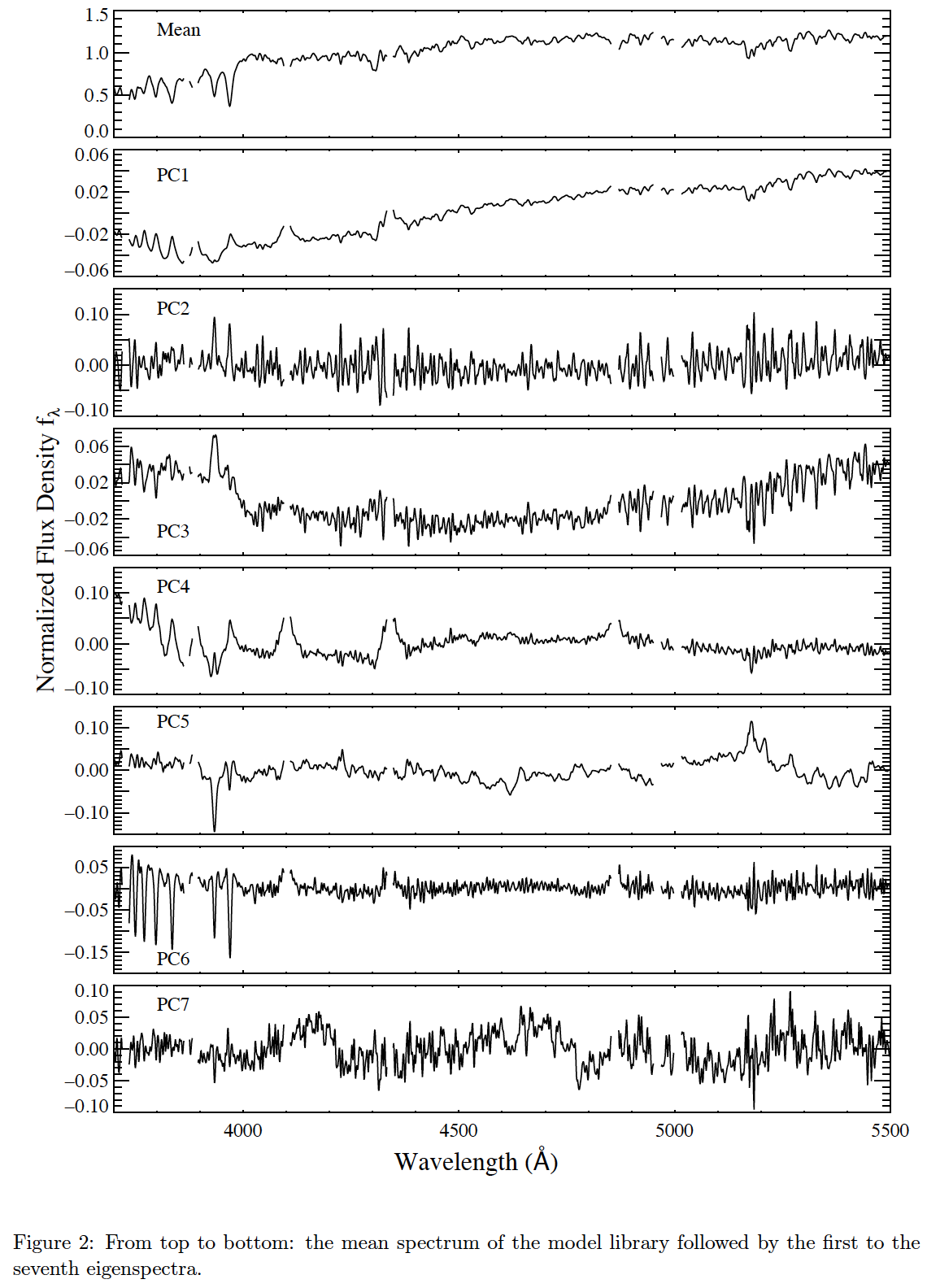
The regions around nebular emission lines are masked in the model spectra. We mask 500 km/s around the [OII]3726.03, [OII]3728.82, Hζ3889.05, [NeIII]3869.06, Hδ4101.73, Hγ4340.46, Hβ4861.33, [OIII]4959.91, and [OIII]5007.84 Å lines. Each spectrum in the masked library is normalized to its mean flux between 3700-5500 Å (this is the range we use for analysis). The mean spectrum of the masked library is calculated and subtracted from each of the model spectra.
PCA code is run on the “residual” spectra. Figure 2 presents the mean spectrum and the top seven PCs for the input model library.
Project BOSS data and models onto PCs
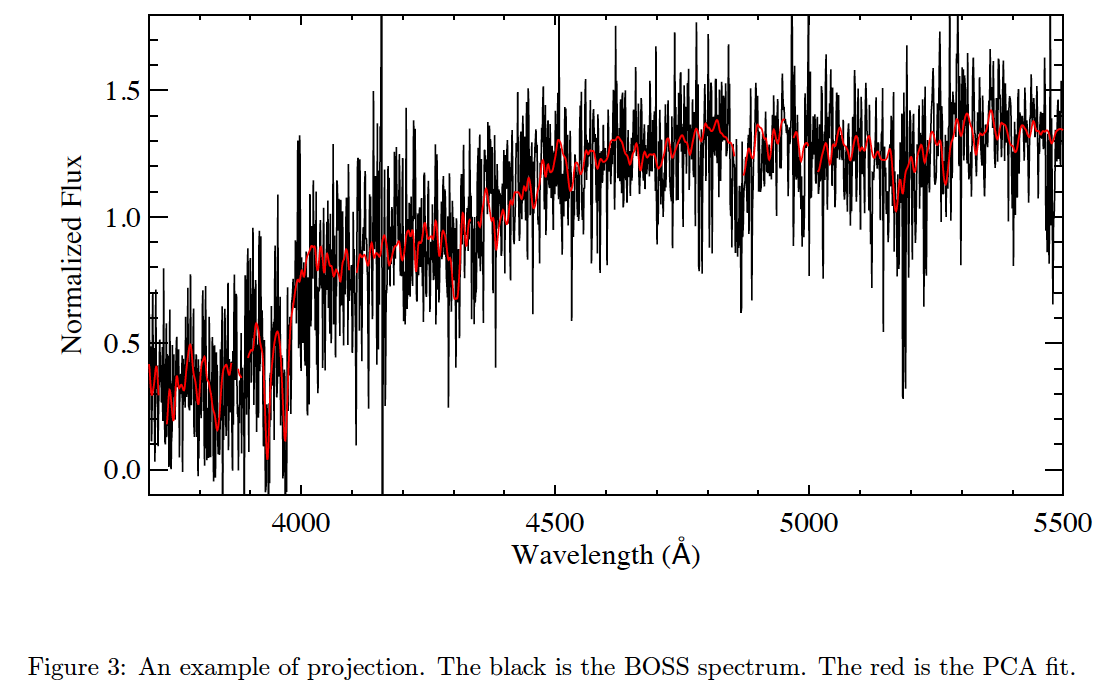
Figure 3 shows an example of projection. The black is the BOSS spectrum. The red is the PCA fit, it is a linear combination of the mean spectrum and the PCs, namely, fit = mean + C1 × PC1 + C2 × PC2 + … + C7 × PC7, where Cα (α = 1–7) are the coefficients of the projection.
Estimate galaxy physical parameters for BOSS
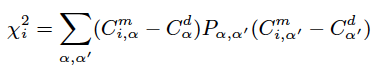
where Cα (α = 1–7) represents the projection coefficients. The superscript “m” and “d” refer to model and data. i represents the i-th model. Pα,α′ is the inverse of the covariance matrix of Cα. The covariance matrix of Cα is calculated in the projection process.